机器学习笔记(4)：线性判别分析

线性判别分析的代码实现参考GitHub

先来回顾一下协方差矩阵的概念。
1. 方差
方差用来衡量 单一变量 的数据有多么分散。数学上表示为 $Var(X)$ 。
2. 协方差
将一个变量从一个增加到两个，就引出了协方差。

协方差是做什么的？ 它用来衡量 两个变量 如何 协同变化。也就是说，当一个变量变化时，另一个变量是倾向于朝相同方向变化，还是相反方向变化。
三种情况：
1. 正协方差 (Positive Covariance): 当变量X增大时，变量Y也倾向于增大。我们称之为“正相关”。
2. 负协方差 (Negative Covariance): 当变量X增大时，变量Y却倾向于减小。我们称之为“负相关”。
3. 零协方差 (Zero Covariance): 两个变量之间没有明确的线性关系。

核心： 协方差描述的是两个变量之间的方向关系。数学上表示为 $Cov(X,Y)$。

3. 协方差矩阵
当有多个变量时，我们需要有一个工具来同时展示所有变量两两之间的协方差关系。

协方差矩阵是做什么的？ 它是一个方阵（行数和列数相等），整齐地排列了多个变量中，每一对变量之间的协方差。

矩阵的结构： 假设我们有三个变量：X, Y, Z。那么协方差矩阵就是一个 3x3 的矩阵。

对角线上的元素 (Diagonal Elements): 对角线上的值是 每个变量自身的方差。因为一个变量和它自己的“协同变化”程度，就是它自身的分散程度（方差）。所以 $Cov(X,X)=Var(X)$。
非对角线上的元素 (Off-diagonal Elements): 非对角线上的值是 不同变量两两之间的协方差。
结构示例： 对于变量 X, Y, Z，其协方差矩阵看起来是这样的：

$$ \begin{bmatrix} Var(X) & Cov(X) & Cov(X,Z) \\ Cov(Y,X) & Var(Y) & Cov(Y,Z) \\ Cov(Z,X) & Cov(Z,Y) & Var(Z) \end{bmatrix} $$

重要特性：对称性 (Symmetry) 。这个矩阵是对称的。因为X和Y的协方差 $(Cov(X,Y))$ 与Y和X的协方差 $(Cov(Y,X))$ 是完全一样的。所以矩阵中，位置 (i, j) 的元素和 (j, i) 的元素是相等的。

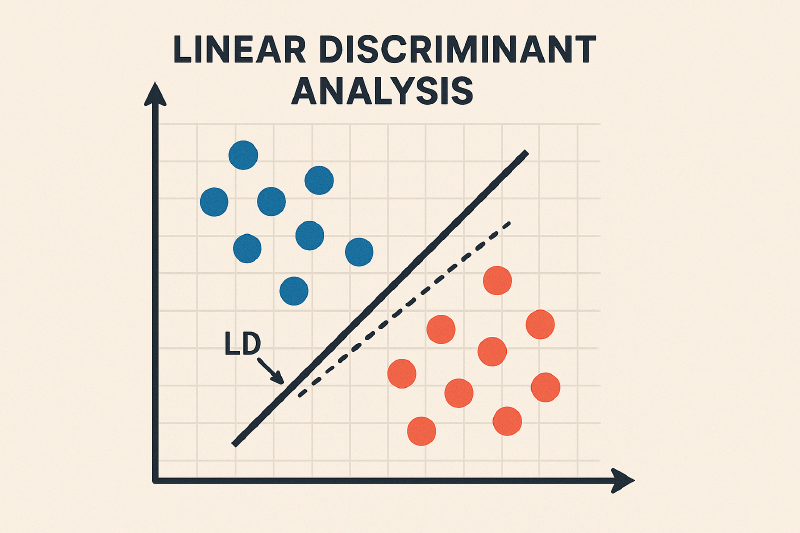
线性判别分析

线性判别分析 (Linear Discriminant Analysis, LDA) 是一种经典的线性学习方法，其思想非常朴素：简单来说，LDA 试图找到一种看待数据的方式 (一个视角或者一个投影) ，在这种方式下，不同类别的数据点能够被最清晰地分开。

LDA 的核心思想是：

“类间距离最大化，类内方差最小化”
(Maximize the distance between classes, and minimize the variance within each class.)

我们把它拆开看：

类内方差最小化 (Minimize Within-class Variance):
- 我们希望同一个类别的数据点，在投影到新的维度后，它们的分布尽可能地集中和紧凑。就像把原来散开的队伍，重新整队变得密集一样。这表示“高内聚”。
类间距离最大化 (Maximize Between-class Distance):
- 我们希望不同类别的数据中心点，在投影后，它们之间的距离尽可能地远。这能让不同类别之间有一道清晰的“鸿沟”。这表示“低耦合”。

LDA 要找的，就是能够同时满足这两个条件的完美投影方向。

LDA 的工作原理

假设我们有一个数据集，包含 $C$ 个类别。

$D_i$ ：第 $i$ 个类别 $ (c_i) $ 的样本集合
$N_i$ ：第 $i$ 个类别 $ (c_i) $ 中的样本数量
$x$ ：一个数据样本，多维列向量
$\mu_i$ ：第 $i$ 个类别的均值向量。
$\mu_i = \frac{1}{N_i} \sum x \{x \in D_i\}$
$\mu$ ：全体样本的均值向量
$w$ ：要寻找的最佳投影方向。投影后的新坐标为 $z = w^Tx$ 。

类内散度矩阵

“类内方差最小化“指的是同一个类别内部的数据点要尽可能紧凑。我们用 类内散度矩阵(Within-class Scatter Matrix) $S_w$ 来衡量这一点。

首先，对于单个类别 $c_i$ ，其散度矩阵 $S_i$ 定义为该类中所有样本点到其均值 $\mu_i$ 的协方差矩阵(乘以常数 $N_i$)。

$$ S_i = \sum_{x \in D_i} (x - \mu_i)(x - \mu_i)^T $$

这里 $(x - \mu_i)(x - \mu_i)^T$ 是一个外积，结果是一个矩阵，它捕捉了数据的分散情况。
然后，我们将所有类别的散度矩阵相加，就得到了总的类内散度矩阵 $S_w$ ：

$$ S_w = \sum_{i=1}^{C} S_i = \sum_{i=1}^{C} \sum_{x \in D_i} (x - \mu_i)(x - \mu_i)^T $$

$S_w$ 综合了所有类别内部的分散程度。我们的目标是让数据在投影后的类内散度尽可能小。

类间散度矩阵

“类间距离最大化”指的是不同类别的中心点要尽可能分开。我们用 类间散度矩阵 (Between-class Scatter Matrix) $S_b$ 来衡量。
$S_b$ 衡量的是各个类别的均值向量 $\mu_i$ 相对于全局均值 $\mu$ 的分散程度，并用该类的样本数 $N_i$ 进行加权。

$$ S_b = \sum_{i=1}^{C} N_i (\mu_i - \mu)(\mu_i - \mu)^T $$

$S_b$ 越大，说明不同类别中心点之间的距离越远。我们的目标是让数据在投影后的类间散度尽可能大。

构建目标函数

现在，我们有了 $S_w$ 和 $S_b$ 。它们都是矩阵，一个矩阵包含了非常丰富的信息：

对角线元素代表了在各个坐标轴方向上的方差。
非对角线元素代表了不同坐标轴之间的协方差(数据分布的倾斜方向和程度)。

这带来了一个核心难题：我们如何判断散度矩阵的“优劣”？我们无法直接比较 $S_w$ 和 $S_b$ 这两个矩阵本身的大小。一个矩阵可能在 X 方向方差大，另一个在 Y 方向方差大，无法简单地说哪个“更优”。所以 LDA 的目标不是在原始的多维空间里进行比较，而是要降维。
简单来说，因为散度矩阵本身描述的是多维度空间中的“总体”混乱程度，而LDA的目标是找到一个“一维”的最佳观察视角（投影线）。因此，我们必须有一种方法来“测量”和“比较”在不同观察视角下，这种混乱程度变成了多少。向量投影 $w^T S w$ 正是完成这个测量的数学工具。
来做一个简单的推导：假设我们只考虑一个类别，它的散度矩阵是 $S = \sum (x-\mu)(x-\mu)^T$ 。

原始数据点：$x$ (一个向量)
投影后的数据点：$z = w^T x$ (一个标量，也就是一维直线上的一个坐标点)
原始均值：$\mu$ (一个向量)
投影后的均值： $\bar{z} = w^T \mu$ (一个标量)

现在，我们来计算投影后这些点 z 的总方差(也就是总散度)：

总方差的定义： $$ \sum (z_i - \bar{z})^2 $$
代入上面的定义： $$ \sum (w^T x_i - w^T \mu)^2 $$
提取公共项 $w^T$： $$ \sum (w^T (x_i - \mu))^2 $$

这里的 $w^T (x_i - \mu)$ 是一个标量。对于任何标量 a，我们都有 $a^2 = a \cdot a^T$。所以：

展开平方项： $$ \sum \left[ w^T (x_i - \mu) \right] \left[ w^T (x_i - \mu) \right]^T $$
根据矩阵转置法则 $(AB)^T = B^T A^T$，我们对第二部分进行转置：$\left[ (x_i - \mu)^T w \right]$
重新组合： $$ \sum w^T (x_i - \mu) (x_i - \mu)^T w $$
提出 $w$： $$ w^T \left( \sum (x_i - \mu) (x_i - \mu)^T \right) w =w^TSw $$

这样，我们就把多维的散度矩阵“压缩”成了一个能够代表投影线上散度大小的标量。

LDA 的目标就是找到一个投影方向 $w$ ，使得投影后的类间散度尽可能大，同时类内散度尽可能小。这自然地导出了一个目标函数，即两者的比值，我们称之为 费雪判别准则 (Fisher’s Criterion)：

$$ J(w)=\frac{投影后的类间散度}{投影后的类内散度} = \frac{w^TS_b w}{w^TS_w w} $$

$J(w)$ 也被称为 广义瑞利商 (Generalized Rayleigh Quotient) 。这时的任务是一个最优化问题，即找到一个 $w$ ，使 $J(w)$ 最大化。

求解最佳投影

由瑞利商的性质，我们实际上可直接得到最佳投影的结果，在这里对其做一定的推导。
注意到，对于一个解 $w$ ，任意缩放 $k \cdot w$ (其中 $k$ 是常数)并不会改变 $J(w)$ 的值，因为分子分母中的 $k^2$ 会被约掉，说明我们只关心 $w$ 的方向，不关心其大小。
因此，我们可以为求解过程增加一个约束条件来固定分母，例如令 $w^TS_w w=1$ ，这样，问题转化为：

$$ \begin{align*} max & \quad w^T S_b w \\ s.t. & \quad w^T S_w w = 1 \end{align*} $$

这是一个典型的 拉格朗日乘数法 (Lagrange Multiplier) 可以解决的约束优化问题，构造拉格朗日函数 $L(w, \lambda)$ ：

$$ L(w, \lambda) = w^T S_b w - \lambda (w^T S_w w - 1) $$

对 $w$ 求导并令其为 0：

$$ \frac{\partial L}{\partial w} = 2S_b w - 2\lambda S_w w = 0 $$

整理后得到：

$$ S_b w = \lambda S_w w $$

通常 $S_w$ 是可逆的，我们可以把它移到左边：

$$ S_w^{-1} S_b w = \lambda w $$

这正是矩阵的广义特征值问题。

$\lambda$ 是矩阵 $S_w^{-1}S_b$ 的特征值。
$w$ 是对应的特征向量。

这个方程的解，就是我们所有局部最优解的集合。

特征值求解与投影

上一节的推导告诉我们，LDA 的优化目标最终归结为一个特征值问题。

* 特征值 $\lambda$ 的意义: 根据瑞利商的性质，每一个特征值 $\lambda$ 都直接对应了其特征向量 $w$ 作为投影方向时的输出 $J(w)$。

全局最优解: 因此，我们不需要担心陷入局部最优。我们只需要遍历所有的特征值，然后找到最大的那一个，其对应的特征向量就是全局最优的投影方向。

求解步骤如下：

根据数据计算类内散度矩阵 $S_w$ 和类间散度矩阵 $S_b$。
求解矩阵 $S_w^{-1}S_b$ 的特征值和特征向量。
将所有特征值从大到小排序：$\lambda_1 \ge \lambda_2 \ge ... \ge \lambda_d$。
根据我们希望降到的维度 $k$，选取前 $k$ 个最大的特征值对应的特征向量，组成一个投影矩阵 $W = [w_1, w_2, ..., w_k]$。

这个矩阵 $W$ 就是我们将数据从高维空间投影到低维空间的“桥梁”。

如何用LDA进行分类

找到了最佳投影矩阵 $W$ 之后，我们不仅完成了降维，还可以用它来进行分类。对于一个未知的新数据点 $x_{new}$：

投影: 将新数据点投影到我们找到的低维空间中： $$ z_{new} = W^T x_{new} $$
计算距离: 分别计算这个新的投影点 $z_{new}$ 到每一个类别中心点的投影 $\mu_{i\_proj} = W^T \mu_i$ 的距离。
判定类别: $z_{new}$ 离哪个类别的中心投影最近，就将其判定为哪个类别。通常使用欧氏距离进行度量。

一个经典对比：LDA 与 PCA

很多人会将 LDA 与主成分分析 (PCA) 混淆，因为它们都能用来降维。但它们的目标和原理完全不同。

特性	线性判别分析 (LDA)	主成分分析 (PCA)
算法类型	监督学习 (Supervised)	无监督学习 (Unsupervised)
核心目标	最大化类别可分性	最大化数据方差 (保留信息量)
是否使用标签	是，必须使用类别标签计算散度矩阵	否，完全不关心类别标签
应用侧重	更侧重于分类任务	更侧重于数据压缩、可视化

简单说，如果降维的目的是为了后续更好地分类，LDA 通常是更好的选择。如果只是想压缩数据，同时尽量不丢失信息，那就用 PCA。

LDA的假设与局限

LDA 虽然强大，但不是万能的，它有一些基本的前提假设：

高斯分布: LDA 假设每个类别的数据都大致呈正态分布（高斯分布）。
同方差性: 经典 LDA 假设所有类别的协方差矩阵是相同且满秩的。如果这个假设不成立（比如一个类别分布是圆形，另一个是细长的椭圆形），LDA 的效果会打折扣。此时，二次判别分析(QDA)可能是更好的选择。
线性可分: LDA 寻找的是线性的决策边界。如果类别间的边界是高度非线性的，LDA 就无能为力了。
对离群点敏感: 由于 LDA 的计算涉及到样本均值和散度，因此离群点（Outliers）会对模型的性能产生较大影响。